Soluciones al control de Sistemas de Ecuaciones (4º ESO-Letras)

Los alumnos de 4º de la ESO (opción letras) pueden comprobar sus soluciones al control con las soluciones aportadas por el profesor (Óscar)

Ejercicio 1:

Ejercicio 2:

Ejercicio 3:

Ejercicio 4:

Ejercicio 5:

Soluciones al control de Trigonometría (4º ESO-Ciencias)

Los alumnos de 4º de la ESO (opción ciencias) pueden comprobar sus soluciones al control con las soluciones aportadas por el profesor (Óscar)

Ejercicio 1:

Ejercicio 2:

Ejercicio 3:

Ejercicio 4:

Ejercicio 5:

Soluciones al control sobre proporcionalidad-3º ESO

Los alumnos de 3º de la ESO pueden comprobar sus soluciones al control con las soluciones aportadas por el profesor (Óscar)

Ejercicio 1:

Ejercicio 2:

Ejercicio 3:

Ejercicio 4:

Ejercicio 5:

Solución del Examen de Recuperación de la 2ª Evaluación (3º ESO)

Ejercicio 1:

Ejercicio 2:

Ejercicio 3:

Ejercicio 4:

Ejercicio 5:

Solución del Examen de Recuperación de la 2ª Evaluación (4º ESO-Ciencias)

Ejercicio 1:

Ejercicio 2:

Ejercicio 3:

Ejercicio 4:

Ejercicio 5:

4º de la ESO - TRIGONOMETRÍA. Ejercicios y Problemas de la página 119 del libro

Ejercicio 39: Responde a las preguntas que se plantean en los 5 apartados (a,b,c,d y e) del ejercicio 39 del libro en la página 119 del mismo.

Apartados y soluciones:

a.- ¿Puede el coseno de un ángulo valer 3/2?

b.- ¿Puede el seno de un ángulo valer 5/4?

c.- ¿Puede la tangente de un ángulovaler 500?

d.- Si un ángulo está en el 2º cuadrante, ¿puede valer su coseno 1/3? ¿Y su seno 1/3?

e.- ¿Puede tener tangente positiva un ángulo que no pertenezca al primer cuadrante?

Ejercicio 40: Calcula los apartados del ejercicio 40 del libro en la página 119 del mismo.

Solución:

4º de la ESO - TRIGONOMETRÍA. Ejercicios y Problemas de la página 113 del libro

Ejercicio 5: Calcula las razones trigonométricas de los ángulos agudos de los triángulos rectángulos de las figuras (Ejercicio 5 de la página 113)

Solución:

Ejercicio 7: Utilizar la calculadora para calcular el valor de unas razones trigonométricas (Ejercicio 7 de la página 113)

Solución:

Ejercicio 8: Con la ayuda de la calculadora calcular los ángulos correspondientes a 2 razones trigonométricas (las cuales vienen en el Ejercicio 8 de la página 113)

Solución:

Problema 11: Una ONG ha decidido construir un puente sobre un río para comunicar dos pueblos de las orillas. Calcula la longitud aproximada del puente con los datos de la figura que viene en el enunciado del problema 11 de la página 113

Solución:

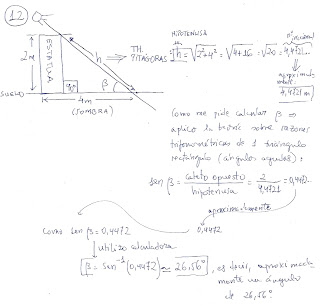
Problema 12 (YA RESUELTO EN CLASE: 20-Abril-2009): Con ayuada de la calculadora, halla el ángulo aproximado que forman los rayos solares con la superficie del suelo en el momento en que una estatua de 2 metros de altura proyecta una sombra de 4 metros (Problema 12 de la página 113)

Solución:

Problema 13 (YA RESUELTO EN CLASE: 20-Abril-2009): La señal de tráfico (mostrada en el enunciado del problema 13 de la página 113) significa que por cada 100 metros que se avanza en la horizontal se sube un desnivel de 13 metros. Con ayuda de la calculadora, halla el ángulo que forma en ese momento la carretera con la horizontal.

Solución:

Teoria sobre el Teorema de Pitágoras-3º ESO

Teoria sobre Reglas de 3 directas-3º ESO

Teoria sobre Media aritmética de valores-3º ESO

Teoria sobre medidas-3º ESO

Teoria sobre Tiempo-3º ESO

Teoria sobre ángulos-3º ESO

Teoria sobre proporcionalidad-3º ESO